Right now, I'm about to state my personal preference for the standard 'chessboard' square array anyway.
The major problem hinges upon moves, and shooting, though corners. If diagonal moves are as 'easy' as orthogonal (as they for a King or Queen in chess), you get the peculiar topography of the chessboard in which the corner-to-corner distance is equal - in effect - as that from side-to-side.
What if you permit only orthogonal movement - or, whenever a move of multiple squares is contemplated, effecting diagonal moves by two orthogonal moves - 1 'up' and 1 'across', for example? The effect of that is almost the same is the problem it seeks to obviate. The range of squares reached from your starting point still describes a square - a smaller one than if diagonal moves were permitted, and it has been tipped up 45deg upon one corner to form a lozenge shape - but it's still a square.
It is possible to mask this effect, as the game Civilization does, by substituting a chequey field by a lozengy one. The picture below is an instance of this sort of thing, with the lozenges flattened along the vertical axis. But it doesn't really resolve the issue.
 |
| Part of the map of Sideon IV, a.k.a. Jono's World. |
My approach is to employ a 'movement allowance' system, in which the 'cost' of moving diagonally is 50% greater than moving orthogonally. This does nothing for movement allowances of just 1 or 2 squares, but for 3 or more, you start to get a 'foorprint' of possible destinations that more closely resembles a circle than the hex system allows.
 |
| Movement Allowances. Please forgive the distortions - this was adapted from a hand-drawn diagram. |
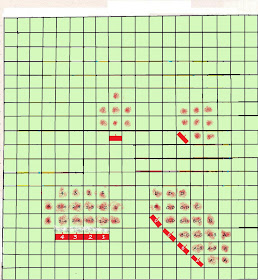
Here we have it. Leutnant Gruber's little tank, sitting in the centre of that array of squares can reach squares depending on its movement allowance (MA), indicated by colour and number. If its MA is 9, then he can reach any coloured square he likes. If it happens to be 5 only (say) then he can reach only as far as the orange squares. Note that I have numbered only along the orthogonals and diagonals from Leutnant Gruber's little tank.
The blue circle shows how close to a circle the MA=7 'footprint' is. The slight penalty for diagonal movement (40% is mathematically much, much the better approximation than 50%, but defeats practicality, methinks) isn't worth troubling about. In my view it is a great advance upon the chess or orthogonals-only systems.
The main difficulty I see at this point is having to 'count by one-and-halves' for diagonal movement. The simple way around this is to double the MA numbers, such that between adjacent squares, an orthogonal move costs 2 Movement Points (MP) and a diagonal move costs 3 MP. Simple: saves fractions, and is easy to remember. So long as one does remember it.
The question now comes down to multi-element units, orientation and musketry ranges and arcs of fire. From the point of view of orientation, I think we will have to accept an artificiality imposed upon us by the grid system: The unit's elements will have to be facing orthogonally or diagonally. In each case, the elements' firing arcs will be defined - for instance - as in the following diagram, in which the shooters' range is measured in the same terms as movement rates: MP.
In the diagram, shooting range is 3 in all cases, but with a limit to how far to a flank. Here, I use the convention of imagining an adjacent element with the same facing. The arc of fire extends to the flank only to a square directly to the front of that adjacent element. That will mean a single element facing diagonally will cover one extra square, but I think we might be in swings and roundabouts country here.
Consider two 4-element units - They might be a 4-company Napoleonic Battalions - in a fire fight. Let their effective musketry range be 3(MP). See how the unit's effectiveness falls away to a flank and beyond 2/3 maximum range to the front.
The unit facing diagonally necessarily covers more front (40% more, geometrically speaking; 50% more in terms of our MP system). As such, you will observe that it covers more squares: 20 to the orthogonally placed unit's 16. If you count the coverage of each square, the right-hand unit scores 32 (4x8) on 20 squares; the left-hand unit 28 (4x7) on 16 squares. The former has the wider coverage (32 to 28), the latter is slightly denser (1.75 per square vs 1.6). Swings and roundabouts. So far, I see no way around this.
For the sake of illustrating any amendments you might care to make, I have added for this diagram 1 MP to the shooting range of our elements. At this point I'll do no more than observe again that the apparent advantage in ground coverage of the diagonal placing is partially offset by the greater density offered by the orthogonal placing (though there the difference is very small). This can be fudged either way. You might decide, for instance, that if a unit can bring any fire to bear upon an enemy, then the whole unit can have a go.
At any rate, I leave this with you for what it is worth. For mine, I'm quite intrigued by the effects of range and arc of fire in concentrating the greater fire effectiveness towards the centre-front. Now, if I could just think of a way to bring that effect into 'free' table gaming, without adding too much in the way of tedium...


I was actually thinking of a group of 1 element units not a multi-element unit but the issues are related I think. Picture a SYW battle line with 2 cavalry wings and say 20 battalions and 2 batteries all aligned side by side and facing the same way under orders to maintain their position in the line.
ReplyDeleteArc of fire occasionally troubles me. I am fairly convinced that units can't really engage units that aren't more or less directly in front of them even though the flanks of the unit can usually fire on a slight angle and/or be refuse or wheel forward. However, units aren't actually frozen in time and so unless constrained by other reasons can wheel in a very short time to fire at an enemy off to the flank (like the Garde at Waterloo being flanked by the British.)
In game terms this requires some form of reaction by local unit commnsders and I have gone that route but decided the arc of fire is an easier way of getting the same result.
Certainly, the longer the ranges, the more important it is to deal with the diagonal distortion. I actually don't have a problem counting .5 but the doubling with 2 and 3 pt costs per square should work well, reminiscent of some hex games I've played long ago. It has the side effect of being able to be used for woods etc by adding 1 or 2 etc to the distance depending on the troop type.
I think my suggestions in the diagrams deal with the flanking fire OK, using much the same sort of convention WRG uses: flanking fire extends as far as one element width beyond the element's front, but a shooting element's priority target is that nearest its front. On a gridded table, this translates as 1 square to the immediate flank, as in the diagrams. If opposing single element units are diagonally placed from each other in adjacent squares, maybe they should simply be turned to face each other without any additional MP penalty. The proviso would be that there is no enemy element directly to the front that is in shooting range.
DeleteConsider this situation in isolation: One RED element is facing 2 BLUE, again in adjacent squares. RED is obviously facing 2:1 odds in the ensuing firefight. That to my mind justifies diagonal shooting at this range, at least by the superior side.
I deliberately left the matter of terrain modifications out, though I could see some issues cropping up there. The main one was a penalty that obviated diagonal movement but allowed orthogonal. But I was inclined to accept this as indicating zigzag roads and trails through rough country.
I've never played in a miniature game using a gridded or hex board, though I did see a number of games played at some of the earlier Gen-Cons using the old "Frappe" Napoleonic Rules which used a hex grid. Seemed to work well enough. Company that sold the rules also sold Hex overlays for the gaming table.
ReplyDeleteI have always used a 'free' board myself for table top games, but explored the possibility of gridded maps for campaigns, bringing the action to the table as the events of the campaign indicate.
ReplyDeleteI have, however, seen DBM translated to a hex-board as aboard game. For mine it didn't work, but I'm at a loss to figure out why. More than likely I just didn't play it long enough to iron out the difficulties I was having.
I have also seen a board game translated to a free table game. That did work, sort of. The game being played with 6mm figures, with rifle range 5cm, you suddenly found river crossings a big deal.
One scenario I recall required a Confederate force to storm a bridge crossing. The experience wargamer in command of that sector, having been repulsed twice, gave up in disgust and stalked off. I took it over, massed as many cannon I could scrape together to cover the approaches, and flung across as many troops as I could gather.
Well, my guys got across, but it was touch and go, for sure.
Archduke Piccolo our group has been using squares on the battlefield for several months and really enjoy the way the game plays. It eliminates a lot of cheesy movement and firing distances. I really like your chart showing possible movement option, a picture really does save a thousand words. Thanks for sharing...
ReplyDeleteThanks, Capt Bill. The main reasons for the diagrams was to 'suck it and see', and because I couldn't figure out how to express it in words!
DeleteThat such systems obviate the fudge and cheese factors to a large extent is gradually persuading me that it is the way to go for the sort of games I might in future be playing.
Cheers,
Ion